5.1 recta tangente y recta normal a una curva en un punto, curvas ortogonales
Una recta tangente a una curva en un punto, es una recta que al pasar por dicho punto y que en dicho punto tiene la misma pendiente de la curva. La recta tangente es un caso particular de espacio tangente a una variedad diferenciable de dimensión.
Sea  una curva, y
una curva, y  un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en
un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en  la curva no cambia repentinamente de dirección. La tangente a
la curva no cambia repentinamente de dirección. La tangente a  en
en  es la recta
es la recta  que pasa por
que pasa por  y que tiene la misma dirección que
y que tiene la misma dirección que  alrededor de
alrededor de  .
.
 una curva, y
una curva, y  un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en
un punto regular de esta, es decir un punto no anguloso donde la curva es diferenciable, y por tanto en  la curva no cambia repentinamente de dirección. La tangente a
la curva no cambia repentinamente de dirección. La tangente a  en
en  es la recta
es la recta  que pasa por
que pasa por  y que tiene la misma dirección que
y que tiene la misma dirección que  alrededor de
alrededor de  .
.
La tangente es la posición límite de la recta secante (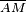 ) (el segmento
) (el segmento 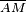 se llama cuerda de la curva), cuando
se llama cuerda de la curva), cuando  es un punto de
es un punto de  que se aproxima indefinidamente al punto
que se aproxima indefinidamente al punto  (
( se desplaza sucesivamente por
se desplaza sucesivamente por 
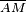 ) (el segmento
) (el segmento 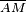 se llama cuerda de la curva), cuando
se llama cuerda de la curva), cuando  es un punto de
es un punto de  que se aproxima indefinidamente al punto
que se aproxima indefinidamente al punto  (
( se desplaza sucesivamente por
se desplaza sucesivamente por 
Si  representa una función f (no es el caso en el gráfico precedente), entonces la recta
representa una función f (no es el caso en el gráfico precedente), entonces la recta 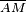 tendrá como coeficiente director (o pendiente):
tendrá como coeficiente director (o pendiente):
 representa una función f (no es el caso en el gráfico precedente), entonces la recta
representa una función f (no es el caso en el gráfico precedente), entonces la recta 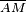 tendrá como coeficiente director (o pendiente):
tendrá como coeficiente director (o pendiente):
Donde 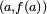 son las coordenadas del punto
son las coordenadas del punto  y
y 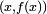 las del punto
las del punto  . Por lo tanto, la pendiente de la tangente TAserá:
. Por lo tanto, la pendiente de la tangente TAserá:
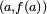 son las coordenadas del punto
son las coordenadas del punto  y
y 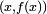 las del punto
las del punto  . Por lo tanto, la pendiente de la tangente TAserá:
. Por lo tanto, la pendiente de la tangente TAserá:
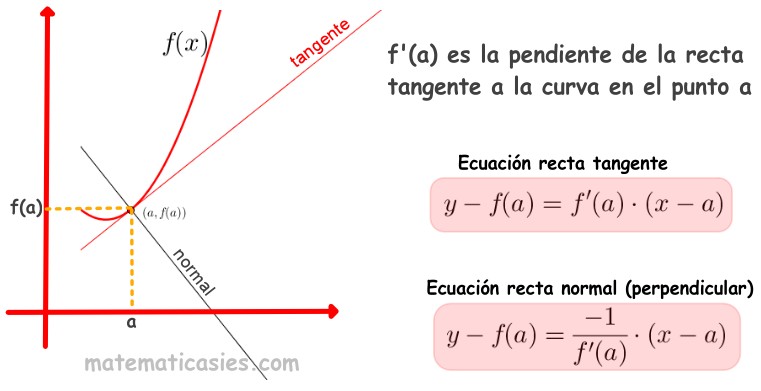
Es, por definición, f '(a), la derivada de f en a.
La ecuación de la tangente es  :
:
 :
:
La recta ortogonal a la tangente 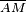 que pasa por el punto
que pasa por el punto 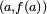 se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por
se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por  . Siendo su ecuación:
. Siendo su ecuación:
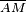 que pasa por el punto
que pasa por el punto 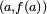 se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por
se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por  . Siendo su ecuación:
. Siendo su ecuación:
suponiendo claro está que 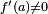 . Si
. Si 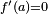 entonces la recta normal es simplemente
entonces la recta normal es simplemente  . Esta recta no interviene en el.
. Esta recta no interviene en el.
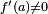 . Si
. Si 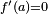 entonces la recta normal es simplemente
entonces la recta normal es simplemente  . Esta recta no interviene en el.
. Esta recta no interviene en el.
5.2 teorema e rolle, teorema de lagrange o teorema del valor medio del calculo diferencial
TEOREMA DE ROLLE
Sea f definida en [a,b], verificando:
- f es continua en el intervalo cerrado [a,b].
- f es derivable en el intervalo abierto (a,b).
- f(a) = f(b).
En estas condiciones existe al menos un punto del interior del intervalo x0 c (a,b) en el que se anula la derivada primera: f´(x0) = 0 ; es decir, la recta tangente a la función en ese punto es horizontal.
TEOREMA DE LAGRANGE o TEOREMA DEL VALOR MEDIO PARA EL CÁLCULO DIFERENCIAL o TEOREMA DE LOS INCREMENTOS FINITOS
Sea f definida en [a,b], verificando:
- f es continua en el intervalo cerrado [a,b].
- f es derivable en el intervalo abierto (a,b).
En estas condiciones existe un punto del interior del intervalo x0 c (a,b) tal que 

5.3 funcion creciente y decreciente maximos y minimos de una funcion, criterio de la primera derivada
5.4 Análisis de la variación de funciones
Cuando la variación total de cualquier función particular es finita, en ese caso, esa función se conoce como Función de Variación Acotada, que puede ser abreviada como función BV (Bounded Variation por sus siglas en inglés). El gráfico correspondiente de la función BV se dice entonces que se comporta bien en un sentido preciso. La función BV tiene amplias aplicaciones en el campo de las matemáticas, y es utilizada en algunos de los teoremas más importantes, tal como son los Teoremas de Fourier. En el caso de la funciones continuas que contienen sólo una variable, la variación acotada implica la distancia finita cubierta por un punto a lo largo del eje y. Otra clasificación establece que las funciones de variación acotada, tienen la propiedad de intervalo cerrado, son las funciones que se pueden establecer como la diferencia entre dos monótonas acotadas. -
5.5 calculo de aproximaciones usando la diferencial
Se define en esta sección el concepto de la diferencial, que nos permite representar la derivada como un cociente y hallar el valor aproximado de la variación de una función alrededor de un punto.
La definición esta motivada por el siguiente razonamiento geométrico. Sea P(x0, y0) un punto fijo sobre la gráfica de y = f (x) Tomando el punto P(x0, y0) como origen, se introduce un nuevo sistema de coordenadas cuyos ejes dx y dyson paralelos a los ejes antiguos.
En este nuevo sistema de coordenadas, la recta tangente en el punto P pasa por el origen y en consecuencia, su ecuaci¨®n es bastante simple, a saber: dy = mdx, donde m es la pendiente. Ahora, como la pendiente en el nuevo sistema es la misma que la del antiguo, esto es m = f ¡¯(x), se tiene entonces: dy = f ¡¯(x) dx Lo anterior nos permite dar la definición formal de las diferencial.
La definición esta motivada por el siguiente razonamiento geométrico. Sea P(x0, y0) un punto fijo sobre la gráfica de y = f (x) Tomando el punto P(x0, y0) como origen, se introduce un nuevo sistema de coordenadas cuyos ejes dx y dyson paralelos a los ejes antiguos.
En este nuevo sistema de coordenadas, la recta tangente en el punto P pasa por el origen y en consecuencia, su ecuaci¨®n es bastante simple, a saber: dy = mdx, donde m es la pendiente. Ahora, como la pendiente en el nuevo sistema es la misma que la del antiguo, esto es m = f ¡¯(x), se tiene entonces: dy = f ¡¯(x) dx Lo anterior nos permite dar la definición formal de las diferencial.
5.6 Problemas de optimizacion y de tasas relacionadas




 que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.
que se tome representará el alejamiento horizontal que haga desde el punto en cuestión. y
y 