domingo, 30 de noviembre de 2014

UNIDAD 4 DERIVADAS


4.1 Conceptos de incremento y de razón de cambio, derivada de una funcion

La derivada de una función es un vector que apunta hacia la dirección donde la función ve un mayor incremento en su valor.
A la luz de la afirmación anterior se puede concluir que la derivada de la función es generalmente cero en algunos mínimos locales o máximos locales dado que en esa posición la función no notaincrementos hacia una dirección en particula


a tasa o razón de cambio puede ser constante o no. Una tasa de cambio constante es aquella que no cambia durante un período de tiempo.
Supongamos que la tasa de cambio del número de migrantes de los años 1978 a 1988 es 2.16 mientras que es de 6.9 desde el año 1988 a 2008.
Así podemos notar que en el ejemplo anterior la tasa de cambio no es constante. En tal situación se puede calcular una tasa de cambio promedio en un intervalo.





4.2 la interpretacion geometrica de la derivada 

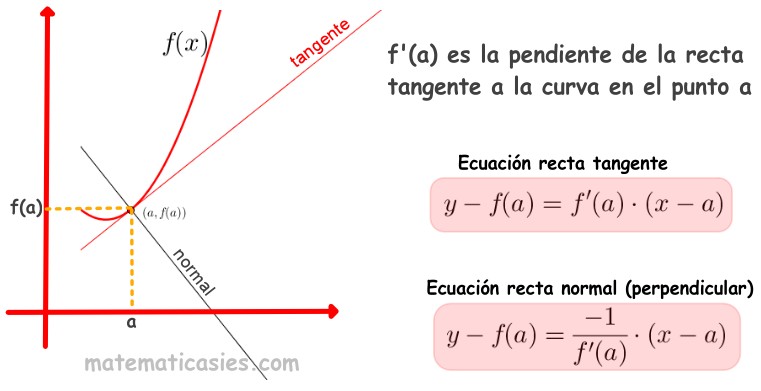
La derivada de una función en un punto es la pendiente de la recta tangente a la función en dicho punto):








4.3 concepto de diferencial,interpretacion de las diferenciales


La forma en que hemos abordado el concepto de derivada, aunque existen varios conceptos, fue el encontrar la relación de la pendiente de la línea recta y´ =f ´(x) que era tangente a la función. Para un punto en particular podemos llegar a la definición de la derivada f ‘(x) y vimos que f ‘(x1) es la pendiente de la recta tangente a la curva en x=x1.
El diferencial se puede tomar en el sentido geométrico como la elevación de la tangente desde el punto en que se toma el diferencial.
Recuérdese que la derivada de la función en el punto es la pendiente de la recta tangente a la función en el punto, como sabemos que la tangente de un ángulo es igual al cociente entre el cateto opuesto (incremento de y) y el cateto contiguo (incremento de x) de un hipotético triángulo rectángulo, sólo hay que despejar el incremento de y que equivale a nuestro diferencial.
Vista geométricamente, la elevación se produce verticalmente a partir del punto en que se toma el diferencial. El incremento  \Delta x \, que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.
Así la elevación de la tangente que se obtenga como resultado dependerá del punto en cuestión y del alejamiento horizontal que se tomen, que en la formulas matemáticas están definidos respectivamente por x \, y \Delta x \,.





4.4 propiedades de la derivada









4.5 Regla de la cadena


Calcular la derivada de la función h(x) = sen x2.

Resolución:

· La función sen x2 es una función compuesta de otras dos f(x) = x2  y g(x) = sen x.

                                       


· Al ser g(x) = sen x, g'(x) = cos x, por tanto g'[f(x)] = cos f(x) = cos x2

              

· Por la regla de la cadena,

h'(x) = g'[f(x)] · f'(x) = 2x cos x2


Resolución:


                                    
                                  
                         


· De g(x) = x3, se deduce g'(x) = 3x2. En consecuencia,

· Por la regla de la cadena,

                                

4.6 formulas de derivacion y formulas de diferencial


da del cociente de una funcion dividida por una constante es igual a la derivada de la funcion dividida por la constante


'Fórmulas de Integración y Diferenciación'


4.7 derivadas de origen superior 


Sea f(x) una función diferenciable, entonces se dice que f '(x) es la primera derivada de f(x). Puede resultar f '(x) ser una función derivable, entonces podriamos encontrar su segunda derivada, es decir f(x). Mientras las derivadas cumplan ser funciones continuas y que sean derivables podemos encontrar la n-ésima derivada. A estas derivadas se les conoce como derivadas de orden superior.
Se utiliza la siguientes notaciones para representar las derivadas de orden superior

1ra Derivada

{f}'_{(x)} ; \frac{\mathrm{d} }{\mathrm{d} x} ; D_x[f_{(x)}] ; \frac{\mathrm{d} y}{\mathrm{d} x} ; \dot{y} ; {y}'

2da Derivada

{f}''_{(x)} ; \frac{\mathrm{d^2} }{\mathrm{d} x^2} ; D_{xx}[f_{(x)}] ; \frac{\mathrm{d^2} y}{\mathrm{d} x^2} ; \ddot{y} ; {y}''

3ra Derivada

{f}'''_{(x)} ; \frac{\mathrm{d^3} }{\mathrm{d} x^3} ; D_{xxx}[f_{(x)}] ; \frac{\mathrm{d^3} y}{\mathrm{d} x^3} ; \dddot{y} ; {y}'''

n-Derivada

{f}^n_{(x)} ; \frac{\mathrm{d^n} }{\mathrm{d} x^n} ; \frac{\mathrm{d^n} y}{\mathrm{d} x^n} ; {y}^n
Cuando el orden de la derivada es mayor a o igual a 4 hay ciertas notaciones que ya no se utilizan.


4.8 derivada de una funcion implicita

Funciones implícitas

Una correspondencia o una función está definida en forma implícita cuando no aparece despejada la y sino que la relación entre x e y viene dada por una ecuación de dos incógnitas cuyo segundo miembro es cero.

Derivadas de funciones implícitas

Para hallar la derivada en forma implícita no es necesario despejar y. Basta derivar miembro a miembro, utilizando las reglas vistas hasta ahora y teniendo presente que:
x'=1.
En general y'≠1.
Por lo que omitiremos x' y dejaremos y'

http://www.vitutor.com/fun/4/b_11.html











Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)