el valor absoluto de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de 3 y de -3.
El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.
Desde un punto de vista geométrico, el valor absoluto de un número real  es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real.
es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real.
 es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real.
es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real.
La función valor absoluto una función continua definida por trozos.
Propiedades fundamentales

No negatividad 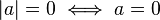
Definición positiva 
Propiedad multiplicativa 
Desigualdad triangular (Véase también Propiedad aditiva)
Otras propiedades

Simetría 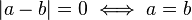
Identidad de indiscernibles 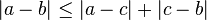
Desigualdad triangular 
(equivalente a la propiedad aditiva) 
Preservación de la división (equivalente a la propiedad multiplicativa)
Otras dos útiles inecuaciones son:
Estas últimas son de gran utilidad para la resolución de inecuaciones, como por ejemplo:
referencia:
Algebra Multimedia.
- Nahin, Paul J.; An Imaginary Tale; Princeton University Press; (hardcover, 1998). ISBN 0-691-02795-1


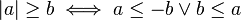



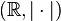 es un
es un
quien es el autor
ResponderEliminar